LIBOR Market Model

Methodology

Fries, Christian: Mathematical Finance. Theory, Modeling, Implementation. Wiley 2007. ISBN 0-470-04722-4.

Spreadsheet (beta version)

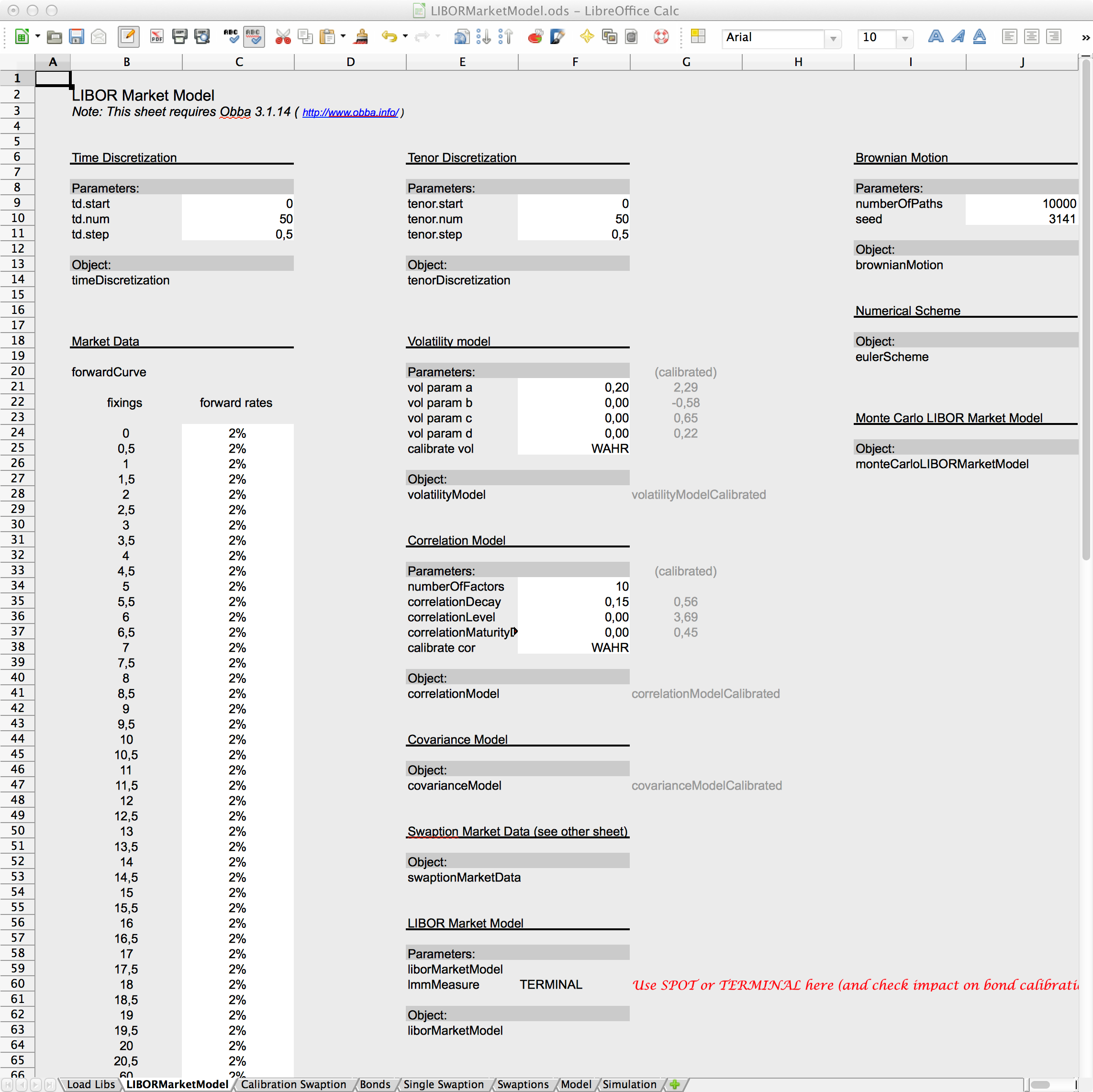
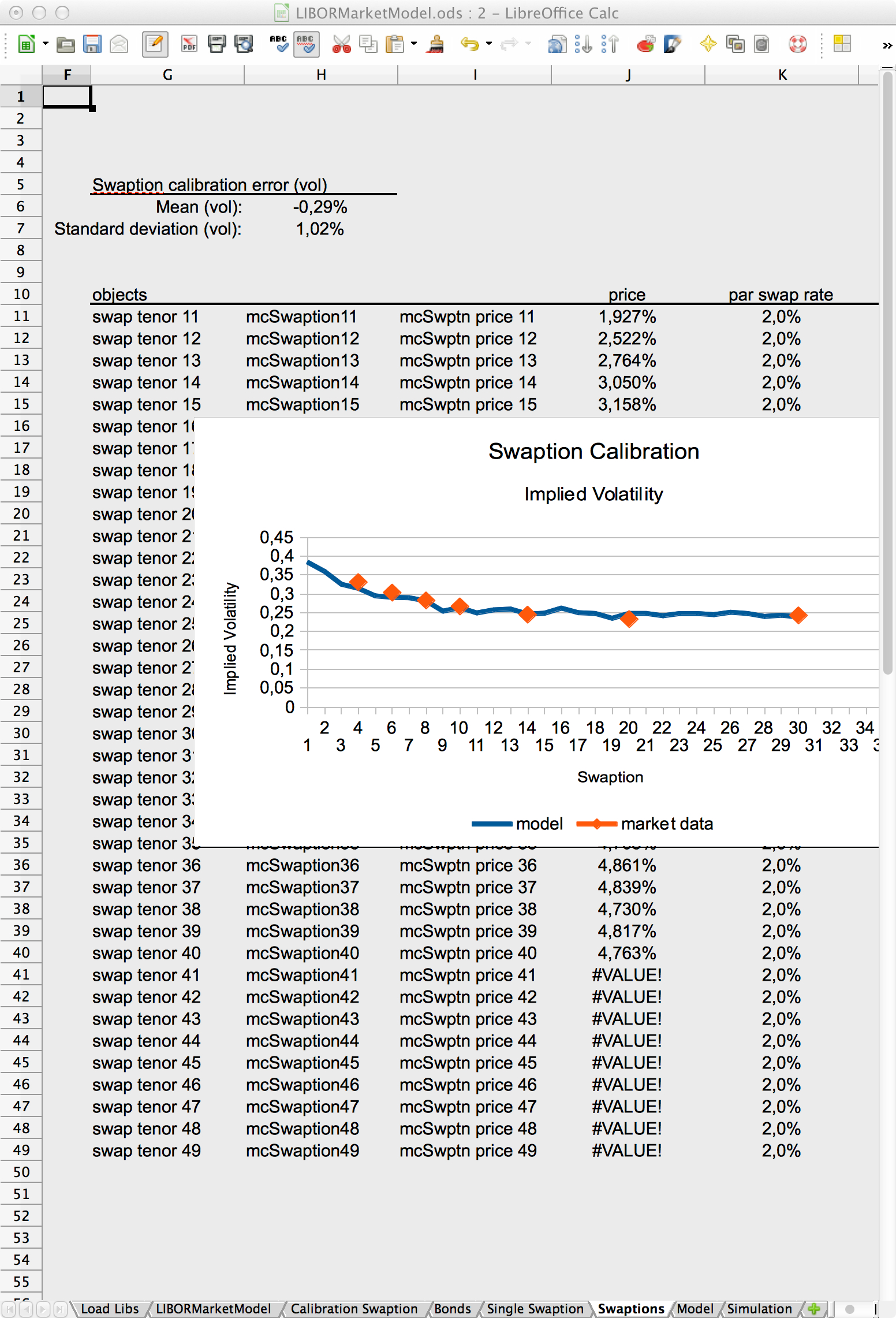
Spreadsheet interface to Java classes related to the LIBOR market model. Left: model specification sheet. Right: Swaption implied volatility calibration.

The spreadsheets are given in Excel (xls) and OpenOffice (ods) format.

In order to run the spreadsheet you have to install the Java Object Handler for Spreadsheets, "Obba".

LIBOR Market Model.zip

LIBOR Market Model

The sheet allows to create a LIBOR market model calibrated to a given forward curve and given swaptions. The parametrised volatility and correlation can be inspected. Generated interest rate scenarios can ben extracted.

Usage

From Spreadsheet

The ZIP archive above contains a spreadsheet which shows creation, calibration and inspection of a LIBOR market model.

Programmatically

The class LIBORMarketModelValuationTest contains some Java code demoing the programmatically creation and calibration of a LIBOR market model. See LIBORMarketModelValuationTest.java

The steps to build and use a LIBOR market model Monte-Carlo simulation are as follows:

1. Create a tenor time discretization: This is the discretization of the forward curve, i.e., the tenor. We create an object implementing the interface TimeDiscretization. Example is an object of class TimeDiscretizationFromArray.
2. Create a forward curve (the initial data of the LIBOR market model): We create an object implementing ForwardCurve, e.g., by creating an object via createForwardCurveFromForwards(), a static method of the ForwardCurveInterpolation class.
3. Create a simulation time discretization: We create an object implementing the interface TimeDiscretization. Example is an object of class TimeDiscretizationFromArray.
4. Create a covariance model, that is the diffusion of the LIBOR market model: We create a covariance model by creating separate volatility and correlation models:
   • Create a LIBORVolatilityModel, e.g., by instantiating an object of class LIBORVolatilityModelFromGivenMatrix or an object of class LIBORVolatilityModelFourParameterExponentialForm.
   • Create a LIBORCorrelationModel, e.g., by instantiating an object of class LIBORCorrelationModelExponentialDecay.
   Create an object of type LIBORCovarianceModelCalibrateable by packing the volatility and correlation model inside a LIBORCovarianceModelFromVolatilityAndCorrelation.
5. Create a LIBORMarketModel from the tenor time discretization, forward curve and covariance model. This object allows to specify the measure (spot measure, terminal measure).
   The covariance model may be calibrated to swaption volatilities by additionally passing calibration object.

1. Create the Brownian motion: Create an object implementing BrownianMotion, e.g., an object BrownianMotionLazyInit from the given simulation time discretization, given number of path and given number of factors.
2. Create the numerical scheme, the process, for the given model and the given Brownian motion, e.g., using EulerSchemeFromProcessModel.
3. Wrap the model and the process into LIBORMonteCarloSimulationFromLIBORModel. This class implements the LIBORModelMonteCarloSimulationModel which is used in product valuation. This object will just provide some convenient methods for obtaining forwards rates.

Source Code

Source code is available from the finmath lib repository, see http://www.finmath.net/finmath-lib.

The framework consists of three parts:

• The implementation of a Monte-Carlo simulation of the LIBOR market model: while there is an extensive set of classes involved, many classes are shared with other models. The model implements the drift and the numéraire, given a diffusion matrix covariance model.
• The implementation of the models instantaneous diffusion matrix. The matrix can be prepresented by a parametric model. The parametric model may perform a calibration to swaptions.
• A collections of products which provide a valuation function expecting a LIBOR Monte-Carlo simulation and perform a valuation.

Monte-Carlo Simulation from Model Specification

Model Specification and Calibration (Different Options for Covariance Modeling)

Product Valuation

Products provide valuation by implementing the AbstractLIBORMonteCarloProduct interface and consuming a model implementing the LIBORModelMonteCarloSimulationInterface interface.

Disclaimer