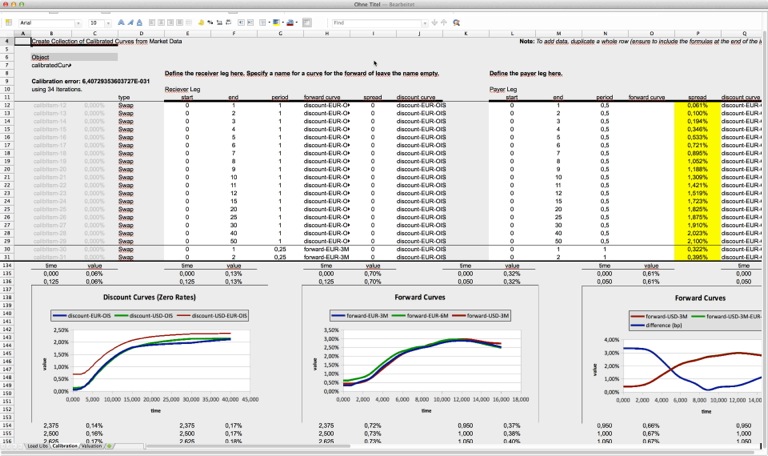
Spreadsheet interface to Java class CalibratedCurves.
The calibration of the model is performed as a multi-threaded global optimization. Hence the calibration greatly profits from a multi-core architecture. It uses as many threads as degree of freedoms (e.g. calibrating 5 curves, each with 20 points will use up to 100 threads).
You may explore the algorithm via a spreadsheet (user perspective) or programmatically by checking out the source code (developer perspective).

Spreadsheet interface to Java class CalibratedCurves.
The spreadsheets are given in Excel (xls) and OpenOffice (ods) format.
In order to run the spreadsheet you have to install the Java Object Handler for Spreadsheets, "Obba".
The sheet calibrates a set of different curves (including discounting curves (e.g., OIS) and forward curves) from swaps. Swaps may feature different discounting curves (e.g., OIS discounting). Forward curves can be calibrated to standard swaps and tenor basis swaps. Discount curves may be calibrated to standard swaps or cross-currency basis swaps.
Although the specific algorithm used is a calibration and not a classical bootstrap, this is sometimes called as curve bootstrapping.
Source code is available from the finmath lib repository, see http://www.finmath.net/finmath-lib.
Below you find a short description about the classes involved in the calibration algorithm. If you like to explore the source code:
The calibration framework consists of three parts:
The curves provide methodology for creating a interpolating curve from a set of points via different interpolation methods on different interpolation entities.
A forward curve can interpolate on the forward value by using its associated discount curve.
Curve are aggregated in an analytic model, which is a collection of curves (Map<String,Curve>) which can be used to evaluate the products.
Products are object carrying the property of the product, including the name of the curves they reference. They provide a function to taking an analytic model (mapping curve names to Curve objects) which returns the value of the product.
The object CalibratedCurves takes a set of calibration specifications and creates all the required curves and calibration products. The result of this process is
Products are valued using an AnalyticModel, which is just a collection of curves (Map<String,CurveInterface>).
The actual optimization is performed by the class Solver. This class returns a modified clone of the provided model containing calibrated version of curves (the original model and the original curves are not modified).
The ZIP archive above contains a spreadsheet which shows a multi-curve calibration (including cross-currency curves) and outputs the calibrated curves.
Below you find some JUnit tests demonstrating how to create curve, calibrate curve and value products programatically. See